10236. N Ферзей – расстановка
Имеется шахматная доска с n * n клетками. Разместите на ней n ферзей таким образом, чтобы ни один ферзь не бил другого.
Вход.
Размер шахматной доски n (1 ≤ n ≤ 10).
Выход.
Если можно разместить всех n ферзей так, чтобы ни один
ферзь не был под ударом другого ферзя, то выведите n строк, содержащих n целых чисел. Целое число в i-ой
строке и j-ом столбце будет обозначать
ячейку (i, j)
доски, и равно 1, если ферзь находится в (i, j)
и 0 в противном случае. Если
имеется несколько способов расположения ферзей, то выведите любую комбинацию.
Если невозможно разместить всех n ферзей желаемым образом, то
выведите “Not possible” (без кавычек).
|
Пример входа |
Пример выхода |
|
4 |
0 1 0 0 0 0 0 1 1 0 0 0 0 0 1 0 |
РЕШЕНИЕ
бектрекинг
Анализ алгоритма
Для хранения
информации о расстановке ферзей на шахматной доске будем использвать двумерный
массив mat:
·
mat[i][j]
= 1, если в позиции (i, j) находится ферзь;
·
mat[i][j]
= 0, если в позиции (i, j) нет ферзя;
Изначально на доске
ферзей нет (mat[i][j]
= 0). Берем первую позицию (1, 1) и ставим на нее ферзя (mat[1][1] = 1). Ищем следующую позицию, например (2, 3), которую не бъет
первый ферзь, и ставим туда второго ферзя. Далее ищем такую
позицию, которую не бъют уже два поставленных ферзя. Такой, например, может
быть (3, 5), куда ставим третьего ферзя.
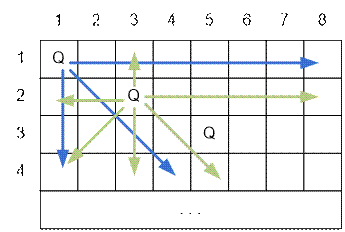
Перебираем позиции (i, j) далее
и ищем такую, в которую можно поставить очередного ферзя. Когда все клетки
доски будут просмотрены, а все n ферзей
расстановлены не будут, начинаем бектрекинг – возврат назад. Пробуем изменить
положение последнего ферзя, найдя ему другое подходящее место. Когда все
позиции этого ферзя будут перебраны, изменяем положение предыдущего ферзя и так
далее продолжаем поиск с возвратом пока не будут расставлены все n ферзей.
Реализация алгоритма
В массиве mat будем генерировать шахматную доску.
int mat[11][11];
Функция attacked проверяет, будет ли атакован хотя бы один ферзь из
позиции (i, j).
int attacked(int x, int y)
{
if (mat[x][y])return 1;
for (int i = 1; i <=
n; i++)
{
if (y - i >= 1
&& mat[x][y - i]) return 1;
if (y + i <= n
&& mat[x][y + i]) return 1;
if (x - i >= 1
&& mat[x - i][y]) return 1;
if (x + i <= n
&& mat[x + i][y]) return 1;
if (x - i >= 1
&& y - i >= 1 && mat[x - i][y - i]) return 1;
if (x + i <= n
&& y + i <= n && mat[x + i][y + i]) return 1;
if (x + i <= n
&& y - i >= 1 && mat[x + i][y - i]) return 1;
if (x - i >= 1
&& y + i <= n && mat[x - i][y + i]) return 1;
}
return 0;
}
Функция print выводит шахматную доску.
void print(void)
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
printf("%d ", mat[i][j]);
printf("\n");
}
}
Функция solve расставляет на доске еще x ферзей так, чтобы они
не били друг друга.
int solve(int x)
{
Если x = 0, то все n ферзей
расставлены. Выводим состояние доски.
if (x == 0)
{
print();
return 1;
}
Перебираем позиции (i, j), проверяем можно ли поставить в (i,
j) ферзя так,
чтобы он не бил уже расставленные.
for (int i = 1; i <=
n; i++)
for (int j = 1; j <=
n; j++)
{
if (attacked(i, j)
== 1) continue;
В позицию (i, j) ставим ферзя.
mat[i][j] = 1;
На остальной доске расставляем x – 1 ферзей.
if (solve(x - 1)) return 1;
Из позиции (i, j) убираем ферзя и совершаем ход
назад (бектрекинг)
mat[i][j] = 0;
}
return 0;
}
Основная часть программы. Читаем размер доски n.
scanf("%d", &n);
Производим расстановку n ферзей.
Если расстановка возможна, то она будет выведена. Иначе выведем сообщение “Not possible”.
if (!solve(n)) puts("Not possible");
Java реализация
import java.util.*;
public class Main
{
static boolean mat[][];
static int n;
static boolean attacked(int x, int y)
{
if (mat[x][y]) return true;
for (int i = 1; i <= n; i++)
{
if (y - i >= 1
&& mat[x][y - i]) return true;
if (y + i <= n && mat[x][y + i]) return true;
if (x - i >= 1
&& mat[x - i][y]) return true;
if (x + i <= n && mat[x + i][y]) return true;
if (x - i >= 1
&& y - i >= 1 && mat[x - i][y - i]) return true;
if (x + i <= n && y + i <= n && mat[x + i][y + i]) return true;
if (x + i <= n && y - i >= 1
&& mat[x + i][y - i]) return true;
if (x - i >= 1
&& y + i <= n && mat[x - i][y + i]) return true;
}
return false;
}
static void print()
{
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
System.out.print(mat[i][j] ? 1 + " " : 0 + " ");
System.out.println();
}
}
static boolean solve(int x)
{
if (x == 0)
{
print();
return true;
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
{
if (attacked(i, j)) continue;
mat[i][j] = true;
if (solve(x - 1)) return true;
mat[i][j] = false;
}
return false;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
mat = new boolean[n+1][n+1];
if (!solve(n)) System.out.println("Not
possible");
con.close();
}
}